声明:本文来自于微信公众号新智元，作者:新智元，授权站长之家转载发布。

【新智元导读】最近的论文表明，LLM等生成模型可以通过搜索来扩展，并实现非常显著的性能提升。另一个复现实验也发现，让参数量仅8B的Llama3.1模型搜索100次，即可在Python代码生成任务上达到GPT-4o同等水平。

强化学习先驱、加拿大阿尔伯塔大学CS系教授Rich Sutton曾在2019年写下一篇名为《The Bitter Lesson》的博文，成为AI领域的经典论述之一。

甚至，Rich Sutton在字里行间体现出的直觉已经颇有Scaling Law的意味。

原文地址:https://www.cs.utexas.edu/~eunsol/courses/data/bitter_lesson.pdf

文章简要回顾了AI在象棋、围棋、语音识别和视觉等领域的发展道路，并提出了这样的观点:

我们应该吸取的惨痛教训之一，就是要意识到通用方法的力量。随着可用算力猛增带来计算量的增加，这种方法可以持续扩展。似乎能以这种方式进行任意扩展的两种方法正是搜索（search）和学习(learning)。

然而，这个观点和Scaling Law并不完全一样，我们也不能以此为据，认为小型模型注定无关紧要。

正如Sutton所描述的，扩展这条路上我们有两板斧:学习和搜索。

OpenAI提出的Scaling Law更强调前者。在其他条件不变时，较大的模型表现更好，因为可以从训练集中学习到更多知识和模式。

但我们往往忽略的是后者。搜索方法也可以在推理阶段随算力增长进行平滑的扩展，以生成更多或者更高质量的候选答案。

斯坦福、牛津、DeepMind等机构的学者最近发表的一篇文章就关注到了这一点。

论文地址:https://arxiv.org/abs/2407.21787

随着推理阶段重复采样数量的提升，模型在GSM8K、MATH、MiniF2F-Math、SWE-bench Lite等数学、推理、代码领域的性能（即问题覆盖率）都有显著提升。

甚至，二者之间似乎存在指数线性关系，并可以用指数幂律建模，似乎能说明推理阶段缩放定律的存在。

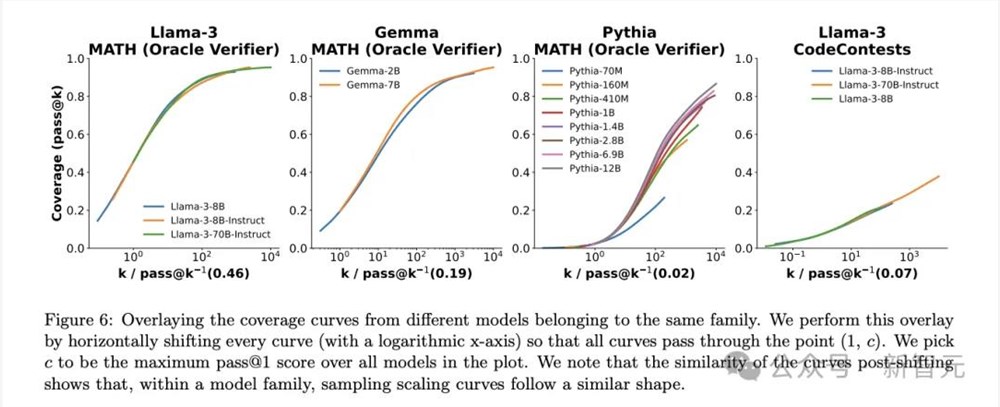
受到这篇论文的启发，两位工程师开始尝试复现——结果是，用100个小Llama模型进行搜索，即可在Python编程任务中追赶甚至打败GPT-4o。

两位作者用了一个形象的比喻:以前，需要一匹马大小的鸭子才能获得边界能力;但现在，我们可以选择用100只鸭子大小的马（或者更确切地说，是羊驼Llama）。

实验所用的源代码已上传至GitHub，而且复现成本相当低。

https://gist.github.com/charlesfrye/27f25188dbbcfdf20a83c0230020fe05

为了尝试较高性能，作者使用了vLLM库实现批量推理，并将硬件条件扩展到10个A100-40GB GPU，输出速度达到40k token/s。

评估指标和结果

作者选择了上述的Large Language Monkeys论文中未涵盖的基准测试——HumanEval。

这个数据集的好处在于，使用运行测试对生成的代码进行评估，而不需要LLM-as-Judge或人类评估的参与，能更加客观地衡量其正确性。

模型的性能通过pass@k和fail@k两个指标衡量。根据PapersWithCode的报告结果，在零样本推理时，GPT-4o的pass@1成绩为90.2%。

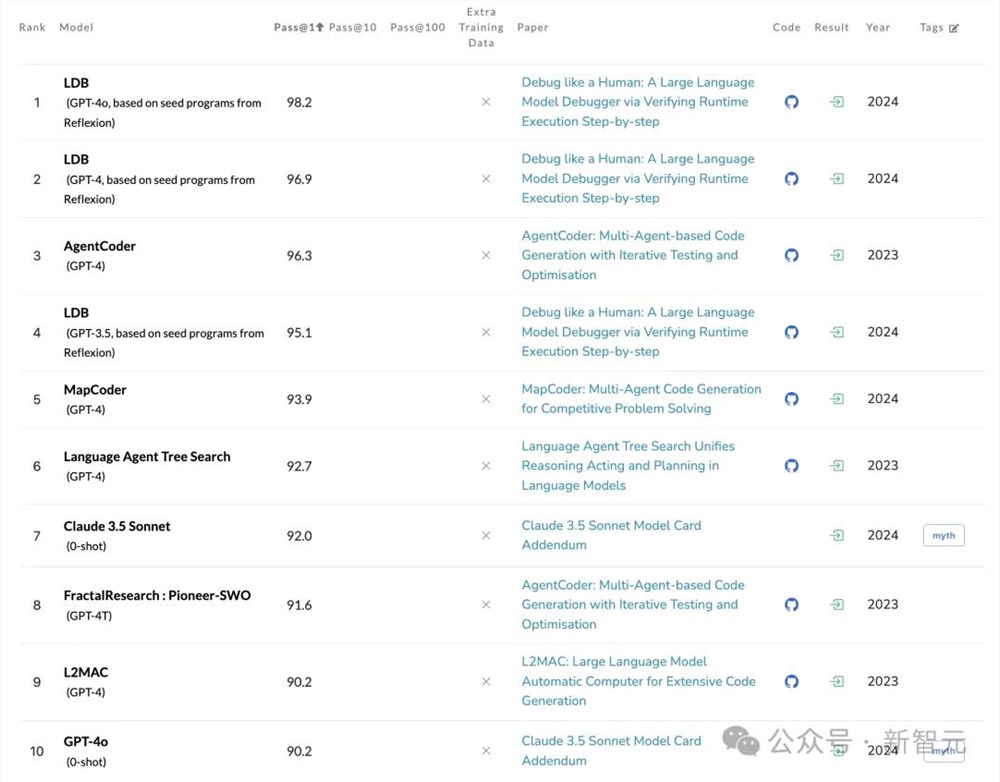
https://paperswithcode.com/sota/code-generation-on-humaneval

使用上述论文提出的方法，加上最少量的prompt微调（未调整其他超参数），Llama3.18B的pass@k分数就有显著提升。

重复采样数k为100时，性能与GPT-4o相当（90.5% vs.90.2%）;k达到1000时，分数为95.1%，明显优于GPT-4o。

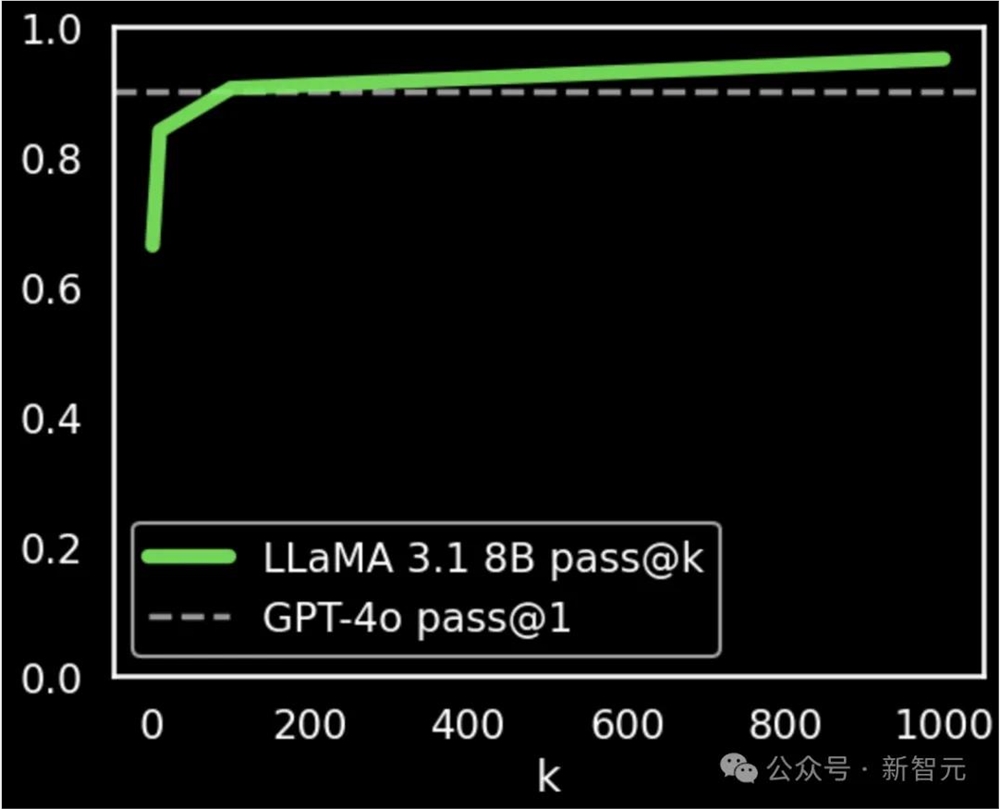
如果使用fail@k指标（相当于1-pass@k），再将上图中的两个坐标轴进行对数变换，就可以看到下图所示的曲线，似乎完美符合「缩放定律」。

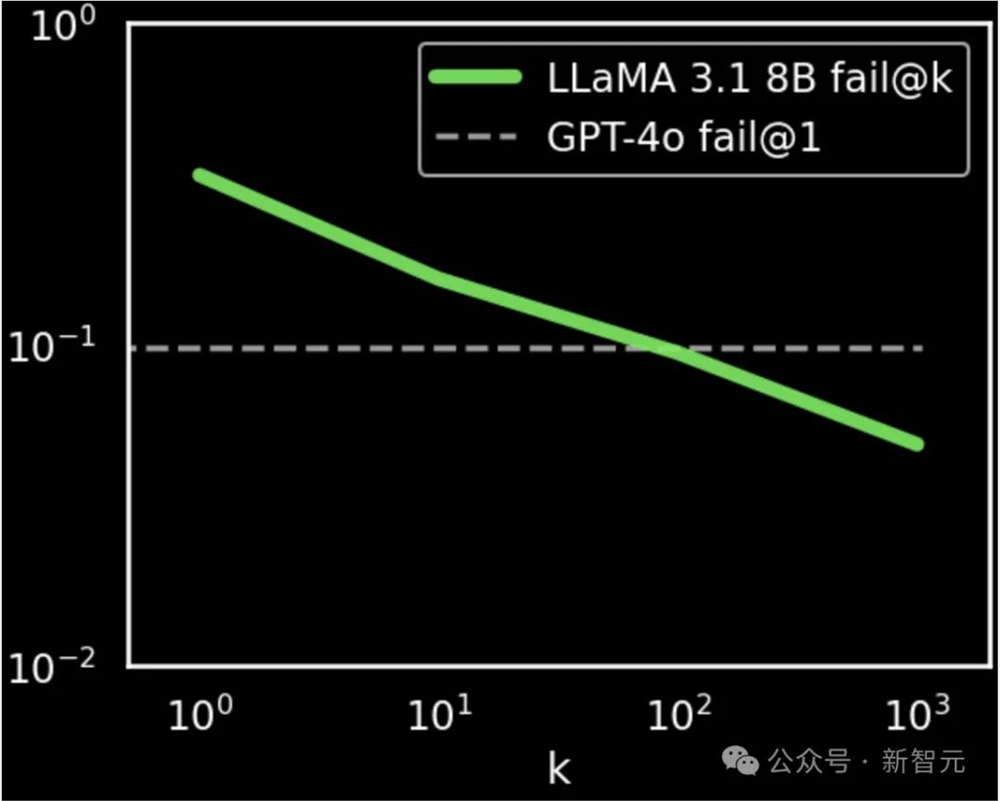
值得注意的是，这个小实验并不是对论文的严格复现，仅是提取了其中的核心方法。

然而，这些结果更加强调了，使用搜索方法进行推理阶段增强时，较小的模型能以可预测的方式胜过GPT-4o这样的「巨无霸」模型。

「搜索」的未来

搜索方法之所以强大，正是因为它能随着计算量的增加进行「透明」的扩展，还可以将资源消耗从内存转移至计算，实现进一步的资源平衡。

最近AI在数学方面的重大成果，比如DeepMind的AlphaProof和AlphaGeometry取得了IMO银牌的水平，以及得到验证的「忙碌海狸」问题，都离不开其中使用的搜索。

然而，搜索的实现首先需要对结果进行高质量的评估。DeepMind的模型将自然语言表述的数学问题翻译为形式化表述，从而得到Lean这种编译器/验证器的详细监督。

陶哲轩也曾在采访中不断强调，「形式化」对AI在数学领域的应用十分重要，可以使并行程度和自动化程度大大提高。

根据Curry-Howard-Lambek对应关系，对数学证明和代码生成结果而言，使用计算机程序进行自动化识别和评估会相对容易。

但类似的方法可能会在数学和编程以外的领域失效。比如，对于「总结电子邮件」这类开放式的NLP任务，就很难进行有效的搜索。

从这个角度来看，搜索是评估的下游。我们可以粗略地预期，生成模型在特定领域中的性能提升，将和评估、搜索能力成正比。

为达到这个目的，可重复数字环境中的agent似乎是一个有前景的方向。

参考资料:

https://modal.com/blog/llama-human-eval